This Blog post is to share takeaways from the Paper “Improving neural networks by preventing co-adaptation of feature detectors”. Code related to this blog post can be found here github repo

Key Ideas:

There are two key ideas presented in the paper , first is dropout itself & the 2nd one is introducing gradient contraints.

1. Dropout

Dropout refers to dropping some neurons from each layer randomly during training time ( paper suggests probability 0.5).

How does that help ?

1. Regularization by preventing co-adaption of neurons
2. Makes training faster , though it might need more epochs to converge
3. Acts as an ensemble . We will discuss this in detail in next section

How does Dropout make the network act approximate as an ensemble ?

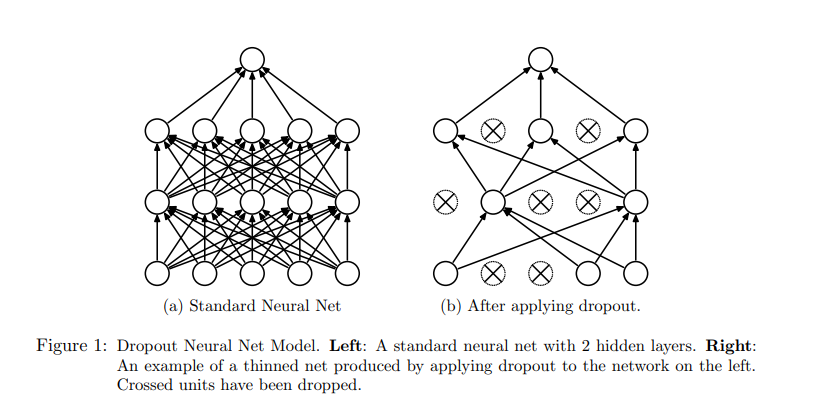
For each minibatch / sample , the network drops random units & learns accordingly. Network in batch1 would not be same as the network being trained in batch2. During inference the activation of the node will be multiplied by probability p again to compensate for removing it.

So instead of training n models over i iterations each , we train 1 model with i’ iterations while still training exponential model architectures over complete training cycle

A proof that mean network is guaranteed to have higher log probabilities than mean of log probabilities of individual network

Assuming the dropout networks do not all make identical predictions, the prediction of the mean network is guaranteed to assign a higher log probability to the correct answer than the mean of the log probabilities assigned by the individual dropout networks - excerpt from the paper

Setup :

1. Imagine we have a neural network with 1 hidden layer of N units and a softmax output layer that computes probabilities over C class labels. This implies there are 2^N possible subnetworks

2. For Each subnetwork \( S_i\) where ( i = 1,…,2^N) , let \(S_{i(c)}\) be probability of class \(c\) as predicted by \(S_i\)

3. Jensen’s inequality for a concave function f , following will hold true : \(f(E[x])>= E(f(x))\)

Using setup rule 3 we know that \(log(E[S(y=c|x)]) >= E[log(S(y=c|x))] .\)

This can be read as follows : log of the probability of mean neural network would be higher than average of log probability of all networks ( recall each network would be different during each mini batch)

Which means that theoritically dropout are supposed to give better results than ensembles of different networks trained during the training process.

2. Gradient constriants:

The idea is that l2 norm penalizes bigger weights , but what if we constraint them to be withing a limit.

How does this help ?

1. We can start with a much larger learning rate & then decay it to converge over iterations. This would help to look in a much larger space & we would ideally not be stuck is a local minima.

Implementing it is fairly staightforward. In case you want to have a look , please refer github repo

Bird eye view of some take aways from the paper

1. Dropout encourages each unit to learn something meaningful from the underlying data by reducing co-adaptation of features
2. Dropout can be used during finetuning models as well . Paper claims finetuning with dropout gives superior results
3. Dropout works better for Layers which are more prone to overfitting ( like Linear Layer)
4. To improve accuracy we can use : a. data augmentation b. using generative pre training to extract useful features from training images without use of labels - Will be trying this out :) , once done would link it here

References:

https://www.youtube.com/watch?v=EeRNywAIYjk https://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf